Di cosa tratta il corso di Matematica Discreta? 

Nel corso di Matematica Discreta si affrontano questioni che, potremmo dire in maniera piuttosto grossolana, hanno a che fare con insiemi finiti o comunque numerabili. Per esempio, in Matematica Discreta ci si può porre la domanda: in quanti modi si può scegliere una password? Esiste una connessione tra due assegnati computer in una rete? Come posso criptare un messaggio in modo che solo il ricevente legittimo possa decriptarlo? Qual è il percorso più breve tra due città in un dato sistema di trasporti? Questo tipo di matematica ha notevoli applicazioni all'informatica, all'ingegneria, ma anche alla chimica, la biologia, la linguistica e alla finanza.

A titolo di esempio ecco qualche problema più specifico che si possono discutere nell’ambito della Matematica Discreta.

Teoria dei grafi. Supponiamo di avere una mappa che mostri la localizzazione di diverse stazioni radio come nella figura seguente:

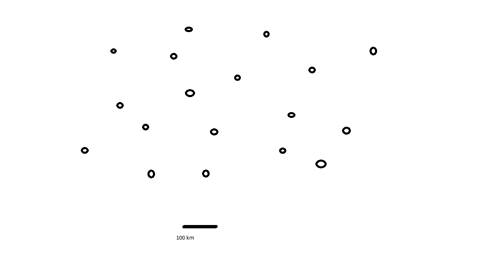
Stazioni troppo vicine devono usare frequenze diverse per evitare interferenze. Quante frequenze diverse dobbiamo usare? Questo problema si presta naturalmente ad essere interpretato mediante la teoria dei grafi.

Combinatoria.

1. Noè ha tre figli: Sem, Cam, Jafet e vuole regalar loro 10 biglietti da 10 euro. In quanti modi lo può fare?

2. Se s è la parte di Sem, c la parte di Cam, j la parte di Jafet, possiamo ordinare queste somme in maniera decrescente (o non crescente) per esempio s ≥ c ≥ j e ovviamente s+c+j=10. In quanti modi si può fare?

3. E se Noè decide che ognuno dei tre debba avere almeno un biglietto da dieci, come cambiano le risposte ai quesiti?

4. Se invece Noè decide di regalare 10 libri ai suoi figli, in quanti modi lo può fare? (Osservare che in questo caso l’ipotesi non detta esplicitamente è che, al contrario di prima, i libri sono tutti diversi mentre i 10 biglietti da 10 euro, pur essendo diversi (diverso numero di serie per esempio) non vengono considerati distinti.)

5. Supponiamo di etichettare i libri come L₁,L₂, …, L₁₀. Sia S l’insieme dei libri dato a Sem, C l’insieme dei libri dato a Cam, J l’insieme dei libri dato a Jafet. Chiaramente i tre insieme S,C,J non hanno mutue intersezioni, e la loro unione e l’intero insieme di 10 libri. In quanti modi diversi si possono scegliere S,C,J?

6. Se Noè vuole che ciascuno dei figli abbia almeno un libro, come cambiano le risposte ai due quesiti precedenti?

7. Come si potrebbero trovare delle risposte a quesiti del genere se invece Noè decidesse di distribuire 1 milione di biglietti da 10 euro a 3000 persone?

Cenni alla Teoria di Ramsey.

Quanto grande deve essere il numero di studenti in questa classe per essere sicuri o che sei di essi siano amici su facebook o che sei di essi non siano amici su facebook?

La Teoria di Ramsey riguarda la possibilità di trovare delle regolarità in un insieme qualunque di dati. Per esempio, se disegniamo dei punti a caso su un piano, con la condizione che tre di essi non siano mai allineati, un certo sottoinsieme di essi forma i vertici di un poligono convesso. Questo, in un certo senso, è analogo al fatto che in un cielo stellato possiamo riconoscere delle costellazioni. Oppure la teoria si può applicare ad analisi di testi. Una stringa sufficientemente lunga di caratteri ha delle regolarità, che possono in parte spiegare perché alcune persone possono scovare “messaggi segreti” all’interno di alcuni testi come la Bibbia.

Teoria dei numeri.

1. Prendiamo un numero intero n maggiore di 1. Se n è dispari prendiamo come intero successivo 3n+1; se invece n è pari prendiamo la metà di n. Ci fermiamo se arriviamo ad 1. Per esempio, cominciamo con 7:

7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1

Cominciamo con 6:

6,3,10,5,16,8,4,2,1

Provare con qualche altro numero tra 2 e 100: si ottiene sempre 1 dopo un numero finito di passi. Magari però esiste un numero più grande per cui il processo non si arresta mai?

2. È difficile trovare il minimo comune multiplo di due interi? Questo si impara alla scuola media e non presenta alcuna difficoltà se possiamo scomporre un numero in fattori primi.

Per esempio, trovare il mcm tra 3417514800 e 1179929104200. Sapendo che

3417514800=2⁴3 5² 7³ 19² 23 mentre 1179929104200=2³ 3² 5² 7² 11³ 19 23² abbiamo allora che il loro mcm è 2⁴ 3² 5² 7³ 11³ 19² 23²=313861141717200. Facile!

Mathematica su un PC, con il comando FactorInteger impiega pochi secondi (circa 30) a scomporre il numero 279594659120932208942141341883843003304057170237252197553939 nei suoi due fattori primi e cioè

671998030559713968361666935769

416064700201658306196320137931

Esercizio: Verificare che il numero 380026694685704762378541836704656635709114742063241198558281345832780770720616003939049360913328894280793070701233239407

è il prodotto di due numeri primi: trovare i due primi.

Mathematica su PC con lo stesso comando di prima non ha trovato i due fattori primi di questo nuovo numero dopo più di 24 ore di calcolo.

Oltre ad una panoramica di questi diversi tipi di problemi, uno degli scopi principali del corso è quello di esercitare o far esercitare anche una abilità di "problem solving", in cui si richiede una qualche creatività nell'applicazione degli strumenti della Matematica Discreta. Infine il corso si propone di sviluppare la capacità dello studente di presentare un’argomentazione corretta.

Tra i vari punti essenziali del corso ci sono dunque: il ragionamento matematico rigoroso; l'abilità di contare oggetti di vario tipo (analisi combinatoria); lo studio di strutture matematiche discrete: insiemi, permutazioni, relazioni, numeri interi, grafi; lo studio di strutture algebriche quali i gruppi, anelli e campi.

Nello specifico, un programma di massima del corso è il seguente:

Numeri interi. Numeri primi. Numeri di Fibonacci. Il teorema fondamentale dell'Aritmetica e alcune sue conseguenze. La funzione di Eulero. La congruenza modulo n . Sistemi di congruenze. Il teorema cinese dei resti. Gruppi. Gruppi ciclici. Gruppi finiti. Il teorema di Lagrange. Il teorema di Cauchy. Il piccolo teorema di Fermat. Il teorema di Eulero. Anelli e campi. Campi finiti. Polinomi, matrici e spazi vettoriali su un campo finito. Elementi di crittocrafia classica e a chiave pubblica. Funzioni aritmetiche unidirezionali. Il  metodo di Diffie e Hellman. Il protocollo RSA. Introduzione ai codici lineari. Teoria delle partizioni di interi. Funzioni generatrici, trasformata zeta. Successioni definite per ricorrenza. Polinomi ortogonali. Identita' soddisfatte da coefficienti binomiali. Formula di convoluzione di Vandermonde. Alcuni risultati generali sugli insiemi finiti. I numeri di Stirling. I numeri di Bell e la formula di Aitken. Il teorema di Pick. Cenni alla teoria di Ramsey.

Grafi finiti. Grafi connessi. Alberi. Il teorema di Cayley. Grafi piani. La formula di Eulero. Il teorema di Kuratowski. Grafi euleriani. Grafi hamiltoniani. La matrice di adiacenza di un grafo finito e le sue potenze. Il polinomio caratteristico di un grafo. Autovalori di un grafo.